Manipulation of Superconducting Vortices at the Nanoscale
Superconductors are well known for their perfect diamagnetism, they expel magnetic flux (see figure 1a). However, that changes if a strong enough magnetic field is applied to them: the flux will thread the superconductor through filamentary regions known as superconducting vortices (figure 2b), each of them carrying exactly one magnetic flux quanta (ϕ0=2.07∙ 10-15 Wb).
Superconducting vortices play a fundamental role in the electrical properties of superconductors, as their motion causes dissipation. Thus, controlling their dynamics is fundamental not only to tailor the electrical properties of superconductors (like reducing dissipation), but also for the development of emerging technologies like superconducting electronics.
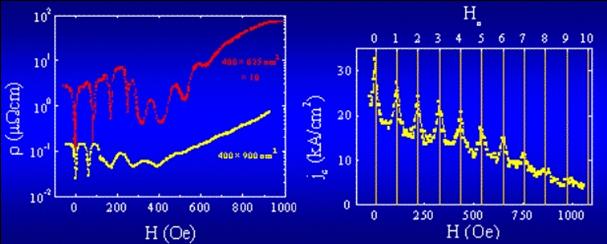
This lab is a pioneer in the control of vortices at the nanoscale. The inclusion of artificially generated pinning centers of sizes similar to the characteristic lengths (such as the coherence lenght) has allowed achieving a great degree of control over the vortex dynamics. For several years we have been studying the commensurability effects (observed in the magnetoresistance and in the critical current dependence with the applied field, see figure 2) induced by periodic arrays of magnetic nanodots in Nb thin films [2,3], and the different pinning mechanisms involved (magnetic, proximity, structural) [4,5,6].
We have also investigated vortex-lattice directional motion guided by periodic potentials [7,8], and quasiperiodic potentials [9]. Another topic we have focused on is the ratchet effect where an asymmetric potential causes an alternating current to rectify and produce a DC voltage [10]. This voltage can be controlled by the amplitude of the current and can actually be forced to undergo a ratchet reversal where the sign of the DC voltage changes [11] (figure 3).
The geometry of the pinning potential plays a fundamental role in how effective vortex pinning is. We have investigated how disorder and different geometries affects the pinning effectivity [12,13]. One of our findings is that conformal lattices provide an optimal pinning strength [14], which could have very significant impact in the design and fabrication of superconducting wires for applications.
[1] M. Vélez, J.I. Martín, J.E. Villegas, c, A. Hoffmann, E.M. González, J.L. Vicent, Ivan K. Schuller, Journal of Magnetism and Magnetic Materials 320(21), 2547 (2008).[2] J. I. Martin, M. Vélez, J. Nogués, and Ivan K. Schuller, Phys. Rev. Lett. 79, 1929 (1997).
[3] O. M. Stoll, M. I. Montero, J. Guimpel, Johan J. Akerman, and Ivan K. Schuller Phys. Rev. B 65, 104518 (2002).
[4] M. I. Montero, Johan J. Akerman , A. Varilci and Ivan K. Schuller, Europhys. Lett. 63, 118 (2003).
[5] E. Navarro, C. Montón, J. Pereiro, A. C. Basaran and I. K. Schuller, Phys. Rev. B 92, 144512 (2015).
[6] A. Gómez, J. del Valle, E. M. González, C. E. Chilliotte, S. J. Carreira, V. Bekeris, J. L. Prieto, I. K. Schuller and J. L. Vicent, Supercond. Sci. Technol. 27, 065017 (2014).
[7] J. E. Villegas, E. M. González, M. I. Montero, I. K. Schuller, J. L. Vicent, Phys. Review B 68, 224504 (2003).
[8] J. E. Villegas, E. M. Gonzalez, M. I. Montero, Ivan K. Schuller, and J. L. Vicent , Phys. Review B 72, 064507 (2005).
[9] J. E. Villegas, M.I. Montero, C.-P. Li and Ivan K. Schuller, Phys. Rev. Lett. 97, 027002 (2006).
[10] D. Perez de Lara, F. J. Castaño, B. G. Ng, H. S. Korner, R. K. Dumas, E. M. Gonzalez, Kai Liu, C. A. Ross, Ivan K. Schuller, and J. L. Vicent, Phys. Rev. B 80, 224510 (2009).
[11] D. Perez de Lara, M. Erekhinsky, E. M. Gonzalez, Y. J. Rosen, Ivan K. Schuller, and J. L. Vicent, Phys. Rev. B 83, 174507 (2011).
[12] Y. J. Rosen, A. Sharoni, and Ivan K. Schuller, Phys. Rev. B 82, 014509 (2010).
[13] C. Chiliotte, G. Pasquini, V. Bekeris, J. E. Villegas, C.-P. Li, and Ivan K. Schuller, Superconductor Science & Technology 24(6), 065008 (2011).
[14] S. Guenon, Y. J. Rosen, A. C. Basaran and I. K. Schuller, Appl. Phys. Lett. 102 252602 (2013)
 Figure 1: Tipical Phase diagram of a superconductor
Figure 1: Tipical Phase diagram of a superconductor 
Figure 2: Conmensurability effect produced by a regular array of pinning centers like the one shown in the inset.
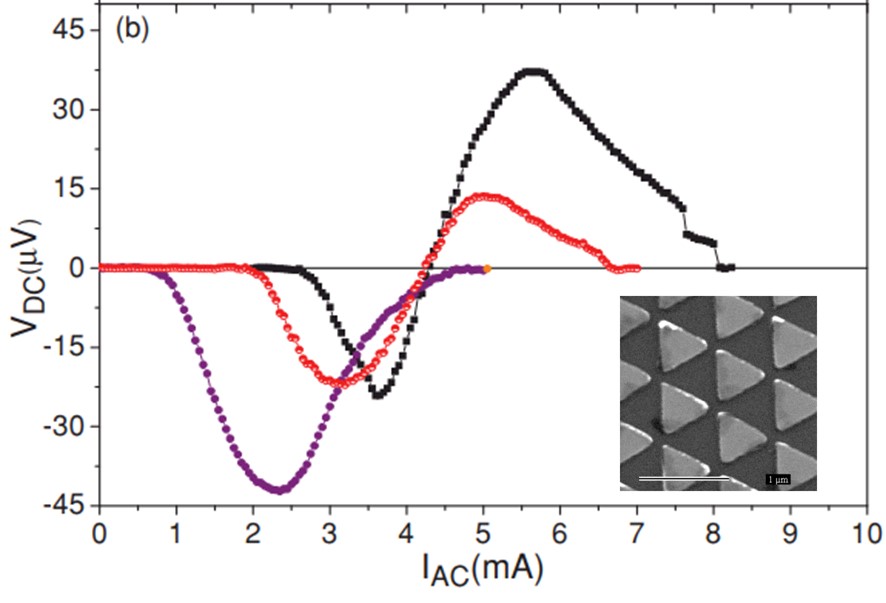
Figure 2: Rectifying effect produced by asymmetric pinning centers like the ones shown in the inset.